#Quantum-enhanced magnetometry
We study how to improve the sensitivity of an optical magnetometer using techniques from quantum optics.
###Spin-squeezing
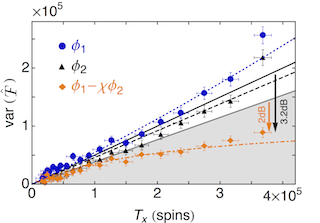
In our paper “Magnetic sensitivity beyond the projection noise limit by spin squeezing” (PRL 109, 253605 (2012)) we demonstrate spin squeezing in an optical magnetometer via quantum non-demolition measurement. We infer 3dB of spin-squeezing, and maintain 90% coherence of the spin state, indicating that we have generated entanglement among the atoms in the sample.
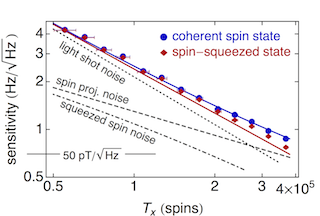
Using the spin-squeezed state, we detect an external magnetic field with sub-projection noise sensitivity. We improve the sensitivity of a 100kHz-bandwidth optical magnetometer by a factor of 10%
###Quantum non-demolition measurement
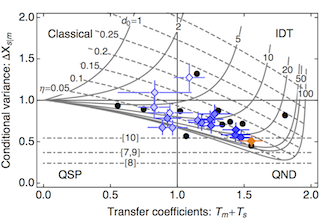
We use quantum non-demolition measurement techniques to generate spin squeezing and entanglement among the atoms. We have described how to adapt statistical tests for verifying if a measurement is truly quantum non-demolition, first developed in studies of optical fields, to measurements of atomic samples (NJP 14, 085021 (2012)), and applied them for the first time in our paper “Certified quantum non-demolition measurement of a macroscopic material system” (Nat. Photon., 7, 517 (2013)).
###Vector magnetometry
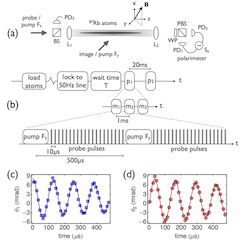
We have developed a simple technique for vector magnetometry using the cold atoms as an in-situ magnetic field probe (APL 102, 173504 (2013)). We monitor the free induction decay signals from two orthogonal polarized input states via paramagnetic Faraday rotation. From these we can reconstruct the magnitude and direction of the external magnetic field, with a measurement bandwidth of 1kHz.
###Planar squeezing
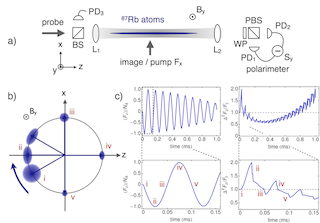
We are interested in extending our spin squeezing techniques to generate a so-called planar squeezed state - i.e. a state squeezed in two orthogonal spin variables. We describe how to do this in our paper “Planar quantum squeezing via quantum non-demolition measurements in cold atomic ensembles” NJP 15, 103031 (2013). Such states would be useful for applications when the optimum measurement phase is unknown, such as tracking a variable magnetic field.